rep-tile – According to The Kidd

INFINITIES 10 – Welcome to the Rep-tile House Part 5 of 5

This is the tenth in a series of posts exploring infinity, entities and ideas infinite, infinities larger than other infinities, infinity paradoxes, infinite perimeters, infinite regress and infinite sequences such as cyclic numbers.

Once again, this post features rep-tiles. A rep-tile (e.g. a square) is a shape which can be divided into smaller copies of itself, and all those smaller copies are the same size.

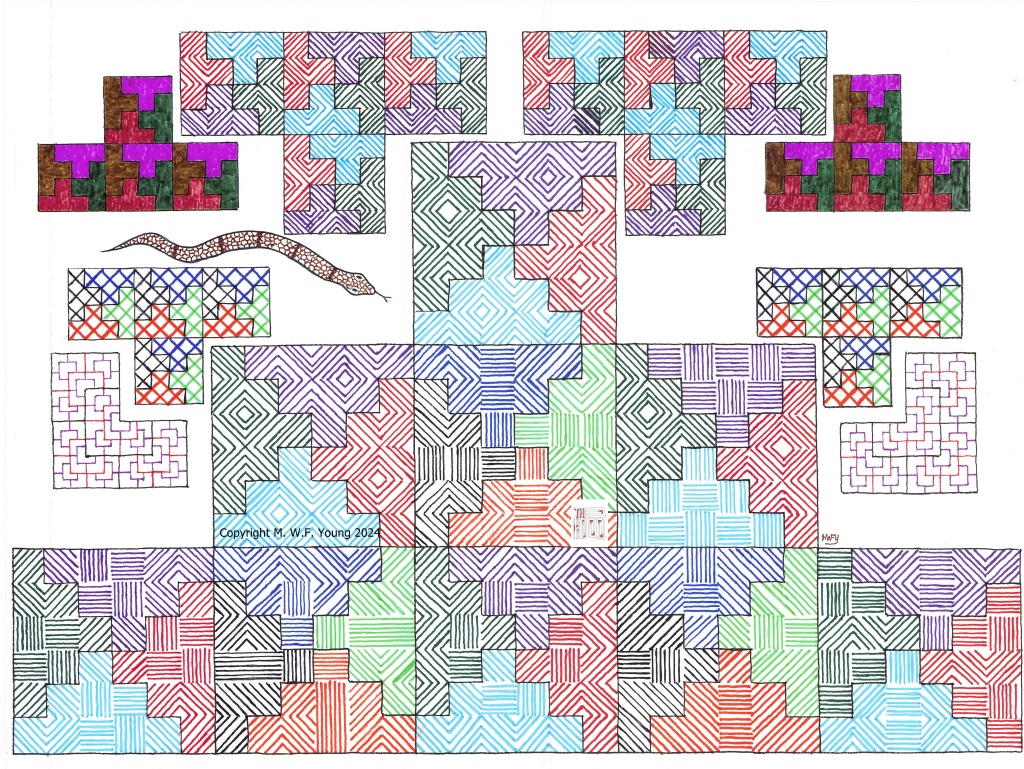
This first illustration features two varieties of rep-tile. The first variety can be seen in the upper left hand corner. A second copy of the same thing can be seen in the lower right hand corner as well:

This rep-tile is made up of nine squares but at the same time four of them can be positioned together to form a perfect square. Therefore this rep-tile is made up of thirty-six equal-sized smaller replications of itself, as pictured. In the upper right hand corner is a second variety of rep-tile, similar to but not the same as the first variety:

A second copy of this variety is also visible in the lower left hand corner. Like the first variety, this rep-tile is made up of nine squares and at the same time four of them can be positioned together to form a perfect square. Therefore this rep-tile, like the first variety, is made up of thirty-six equal-sized smaller replications of itself, as pictured.

There is also an interesting design in the centre:

Here we have four identical crosses. Each cross is divided up into geometric figures called pentominoes. A pentomino is a shape consisting of five connected squares. Five squares can be joined together in twelve different ways. Only nine of those twelve are used in each of these crosses. Before continuing you might want to see if you can figure out what the other three pentominoes are. Here is my illustration of pentominoes within pentominoes:

The twelve black shapes are the twelve different pentominoes. There are three giant pentominoes here forming a giant rectangle, and that rectangle is also divided up into the twelve pentominoes separated by white lines. Each of those twelve are divided into nine smaller pentominoes. Each of those nine are in turn divided into nine smaller pentominoes. The design at the bottom also consists of pentominoes. Here is another work made up of complex groupings of pentominoes:

In this next work I have shown how 12 pentominoes (five squares each) are equal in area to the cross (six squares):

Around the main central figure here is a white frame also made up of pentominoes (and blue circle arcs). Around the outside of that frame is a collection of smaller pentominoes. The panel at the bottom is a demonstration of how the twelve pentominoes can be arranged to form a rectangle in two different ways. In this next work there are brightly covered pentominoes surrounding a blue staircase. That staircase is composed of hexominoes (a hexomino is a shape made up of six squares):

Finally, here is another cross made up of pentominoes and around the outside there are multi-coloured hexominoes.

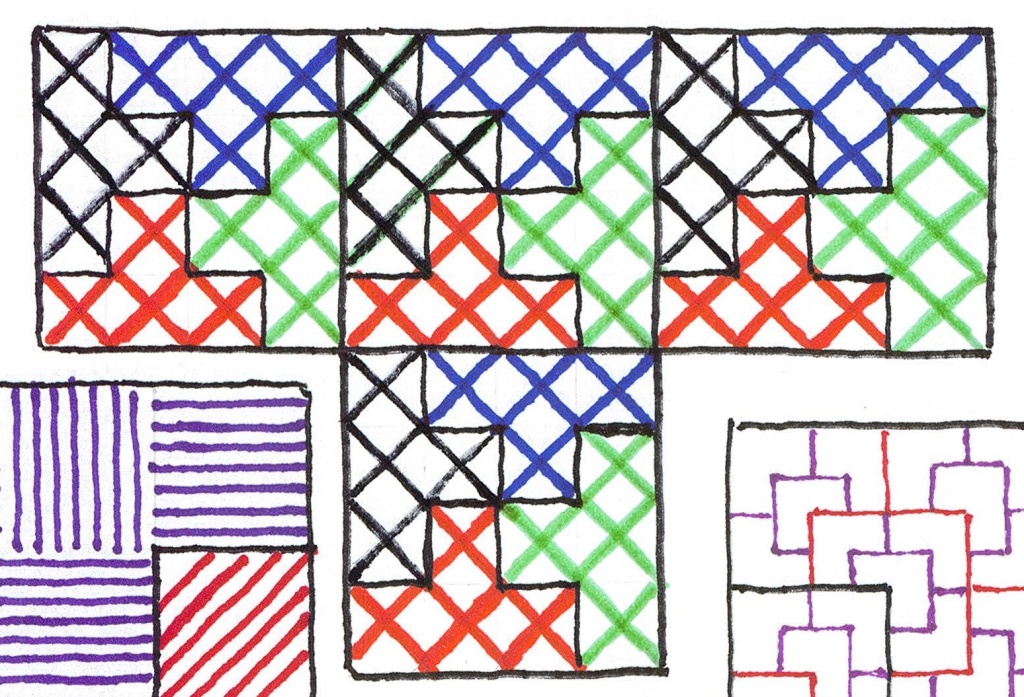
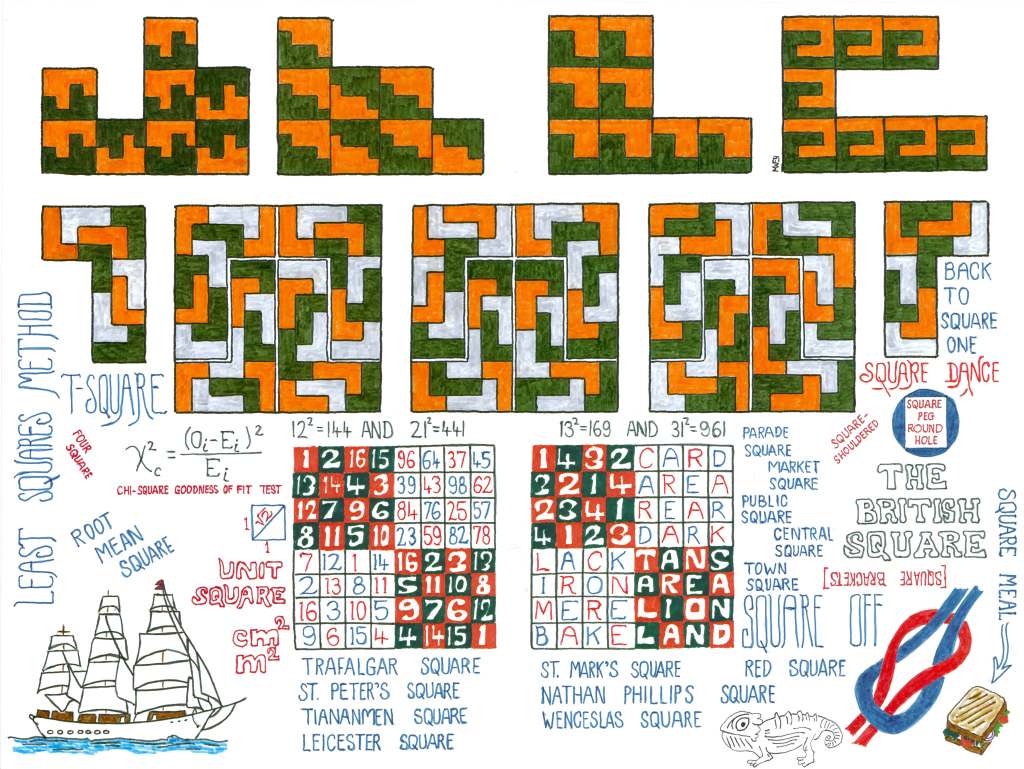
Back to the rep-tiles, here we have one rep-tile in two different sizes and eight different colours:

This rep-tile is made up of nine squares again, basically a rectangle (two squares by four squares) plus a single ninth square projecting out on one side. Once again, four of these rep-tiles can be positioned to form a square. Therefore each rep-tile can be divided up into thirty-six (four times nine) smaller equal-sized rep-tiles identical to the large rep-tile. There is a large version of this on the left side comprised of sharp somewhat dark colours (except for the orange):

Two more smaller versions of this version can be found in the middle. The second version is made up of lighter colours (except for the blue) on the right side, also a large rep-tile consisting of thirty-six smaller rep-tiles:

Two slightly smaller duplicates of this second version can also be seen in the centre, for a total of four rep-tiles in the centre which form a large square:

Finally, here is what I think is the most striking of the rep-tile works discussed in this post. There are two different rep-tiles here:

On the upper left is the first rep-tile:

Each rep-tile here is made up of nine squares, and at the same time one can put four of these rep-tiles together to form a square. Therefore, again, this rep-tile can be divided up into thirty-six (four times nine) smaller equally-sized rep-tiles which are replications of the larger rep-tile. We have four rep-tiles on the upper left, two being black and red and two being white and red. This entire square is duplicated in the lower right. The second rep-tile can be seen on the upper right:

Once again this rep-tile is made up of nine squares, and again four of these rep-tiles can be positioned together to form a square. Therefore, again, this second rep-tile can be divided up into thirty-six smaller equally-sized rep-tiles identical in shape to the large rep-tile. On the upper right we see four rep-tiles, two made up of black and blue rep-tiles, and two made up of white and blue rep-tiles. All of this is duplicated on the lower left.

This is the last of the rep-tile posts but a series of posts on extraordinary irrep-tiles and infin-tiles is in the works for some later date.

Next Post: CYCLIC POWER

Post 1 – Infinity Everywhere – https://thekiddca.wordpress.com/2024/04/06/infinities-infinity-everywhere/

Post 2 – Snowflake Curve – https://thekiddca.wordpress.com/2024/04/13/infinities-2-theres-no-business-like-snow-business/

Post 3 – Ch’i Ch’iao T’u – https://thekiddca.wordpress.com/2024/04/20/infinities-3-infinitesimal-chi-chiao-tu/

Post 4 – Hotel Infinity – https://thekiddca.wordpress.com/2024/04/27/infinities-4-no-vacancies-but-rooms-still-available-at-hotel-infinity/

Post 5 – Pythagorean Infinity – https://thekiddca.wordpress.com/2024/05/04/infinities-5-pythagorean-infinity/

Post 6 – Rep-tiles 1 – https://thekiddca.wordpress.com/2024/05/12/infinities-6-welcome-to-the-rep-tile-house-part-1-of-5/

Post 7- Rep-tiles 2 – https://thekiddca.wordpress.com/2024/05/18/infinities-7-welcome-to-the-rep-tile-house-part-2-of-5/

Post 8 – Rep-tiles 3 – https://thekiddca.wordpress.com/2024/05/25/infinities-8-welcome-to-the-rep-tile-house-part-3-of-5/

Post 9 – Rep-tiles 4 – https://thekiddca.wordpress.com/2024/06/01/infinities-9-welcome-to-the-rep-tile-house-part-4-of-5/

INFINITIES 9 – Welcome to the Rep-tile House Part 4 of 5

This is the ninth in a series of posts exploring infinity, entities and ideas infinite, infinities larger than other infinities, infinity paradoxes, infinite perimeters, infinite regress and infinite sequences such as cyclic numbers.

A shape is a rep-tile if it can be divided up into smaller shapes so that all of those smaller shapes are exactly the same shape as the large shape you started with. All of those smaller shapes must also all be the same size for you to have a rep-tile. This is another post about rep-tiles.

This first illustration is pretty straightforward. There are actually two large rep-tiles here, each one a mirror image of the other though they are coloured slightly differently to differentiate them. Each of the two large shapes consists of eighteen squares. However, each of those squares is divided up into two smaller shapes each of which is identical to the large shape. Therefore, each rep-tile consists of thirty-six identical smaller shapes all the same size and all the same shape as the original large shape:

Of course, like all rep-tiles, one can create an infinite regression. In this case each large rep-tile is made up of thirty-six smaller shapes. Each one of those smaller shapes can therefore be divided up into thirty-six shapes which are even smaller and each of those even smaller shapes can be divided up into thirty-six shapes that are yet smaller. One can do that forever infinitesimally. One can of course go in the opposite direction as well, putting thirty-six copies of the large shape you started with together to make an even larger shape, and continue doing that creating ever larger rep-tiles as long as you want.

It occurred to me, however, that one could generate an infinite sequence of rep-tiles in an entirely different way. In an earlier post I discussed a rep-tile that looks like a sort of giant stubby inverted letter T:

One can take four of these inverted T-shapes and put them together to form a square. Since the inverted T-shape is itself constructed out of four squares, one could take each of those four squares and divide each of them up into four smaller T-shapes giving you sixteen T-shapes all together. One could continue creating smaller and smaller (or larger and larger) T-shapes forever.

One could also see this as a very short two-layered staircase, i.e. one could start on the left side, step up onto the first square, take a second step up onto the top square, then step down onto the last square in the staircase, and then take one final step onto the ground again. Then I wondered whether one could create a three-layered reptilian staircase made out of nine smaller squares, with five squares on the bottom layer, three squares as the second layer, and one square at the top. Going from left to right, one could ascend to the top then descend to the ground again on the right side in six steps. Not only that, but one could take four of these three-tiered staircases and form a large square. Since this staircase is itself made out of nine squares, each of those nine squares could be divided up into four smaller three-tiered staircases so that indeed you have a rep-tile which can be divided up into thirty-six (9 x 4) smaller equal-sized copies of itself.

Here is a design I created whose main feature is such a three-tiered staircase:

Besides the three-tiered staircase, this design also features three examples of rep-tiles comprised of two-tiered staircases – Example 1:

Example 2:

Example 3:

Thrown in for good measure is another rep-tile in the shape of an L which I’ve used in earlier posts:

Now comes the interesting part. One could create a four-tiered rep-tile as well, and a five-tiered and six-tiered and so on getting infinitely larger. This isn’t a case of one particular shape increasing in size infinitely and decreasing in size infinitesimally. The three-tiered staircase is not identical in shape to the two-tiered staircase.

Ever larger staircases can be generated so that four of each one can be combined to form a square, and of course each staircase is itself made up of squares. Therefore a staircase rep-tile made up of n squares can be divided up into 4n smaller identical replications of itself. If n=4 you have a two-tiered staircase, and if you put four of them together you have sixteen squares and not only that but those sixteen squares can be used to generate a four by four array consisting of four staircases. Similarly one can construct a six by six array using four three-tiered staircases (each made up of nine squares) since 4 x 9 = 36 = 6 x 6. Here is a diagram illustrating staircases for n = 16, 25, 36, 49 and 64:

NEXT POST: Welcome to the Rep-tile House Part 5 of 5.

Post 1 – Infinity Everywhere – https://thekiddca.wordpress.com/2024/04/06/infinities-infinity-everywhere/

Post 2 – Snowflake Curve – https://thekiddca.wordpress.com/2024/04/13/infinities-2-theres-no-business-like-snow-business/

Post 3 – Ch’i Ch’iao T’u – https://thekiddca.wordpress.com/2024/04/20/infinities-3-infinitesimal-chi-chiao-tu/

Post 4 – Hotel Infinity – https://thekiddca.wordpress.com/2024/04/27/infinities-4-no-vacancies-but-rooms-still-available-at-hotel-infinity/

Post 5 – Pythagorean Infinity – https://thekiddca.wordpress.com/2024/05/04/infinities-5-pythagorean-infinity/

Post 6 – Rep-tiles 1 – https://thekiddca.wordpress.com/2024/05/12/infinities-6-welcome-to-the-rep-tile-house-part-1-of-5/

Post 7 – Rep-tiles 2 – https://thekiddca.wordpress.com/2024/05/18/infinities-7-welcome-to-the-rep-tile-house-part-2-of-5/

Post 8 – Rep-tiles 3 – https://thekiddca.wordpress.com/2024/05/25/infinities-8-welcome-to-the-rep-tile-house-part-3-of-5/

INFINITIES 8 – Welcome to the Rep-tile House Part 3 of 5

This is the eighth in a series of posts exploring infinity, entities and ideas infinite, infinities larger than other infinities, infinity paradoxes, infinite perimeters, infinite regress and infinite sequences such as cyclic numbers.

Illustration copyright MURRAY YOUNG 2024

This is also the third in a series of posts about replicating tiles, or rep-tiles for short. A rep-tile is a shape (e.g. a square) which can be subdivided into smaller shapes all of which are identical in shape to the figure you started with. Those identical smaller shapes are also the same size. If they were different sizes we’d have an irrep-tile (irregular replicating tile). For more details about rep-tiles see the first post in this series.

In my illustration above, there is a pair of rep-tiles in the centre, one on each side of the entrance to the GRÜNER KÄSE MINING CORPORATION. All four of the smaller shapes on each side are the same shape and size. I wonder what GRÜNER KÄSE means? The LUNAR FLYER, however, is made up of two irrep-tiles (irregular replicating tiles).

The top half, for example, is a large shape identical to both the two somewhat smaller brown shapes and the other eight even smaller multi-coloured shapes, but because these ten smaller shapes are not all the same size this is an irrep-tile rather than a rep-tile. In the same way, the two multi-coloured shapes at the bottom are also irrep-tiles rather than rep-tiles:

It is also interesting to note that the two rep-tiles in the centre, the two irrep-tiles at the bottom and the two irrep-tiles that form the Lunar Flyer can all be subdivided into right-angled triangles with angles of 30^o, 60^o and 90^o, three of them, six of them and four of them respectively.

LACUS TEMPORIS
By NASA (image by Lunar Reconnaissance Orbiter) – JMARS, Public Domain, https://commons.wikimedia.org/w/index.php?curid=41050860

Lacus Temporis is an actual location on the moon, but I just made up the name Lunopolis.

The Palace of the Grand Lunar is a structure mentioned in the ground-breaking science fiction novel ‘The First Men in the Moon’ by H.G.Wells published in 1901 and made into films in 1919 and 1964. One of the two protagonists in that novel is a scientist named Mr. Cavor.

Most of the shapes in the illustration above are rep-tiles. In the left and right corners at the top, however, are two irrep-tiles with smaller and smaller squares eventually becoming infinitesimal:

In this illustration we see two colourful red, orange and green trapezoids at the top which are also rep-tiles, each divided into nine smaller trapezoids:

A trapezoid is any four-sided figure with one pair of parallel sides. In between these two trapezoids it can be seen how one can put three trapezoids together to form an equilateral triangle. Underneath that triangle is another trapezoid made up of smaller and smaller trapezoids which makes this version of the trapezoid an irrep-tile. At the bottom are all manner of some of the less interesting rep-tiles in this world, including:

a rhombus on the far left (four equal sides)
two varieties of right-angled triangles with angles of 30^o, 60^o and 90^o
isosceles right-angled triangles
parallelograms (a quadrilateral with opposite sides parallel)
symmetrical trapezoids
squares
asymmetrical trapezoids
irregular pentagons
an equilateral triangle
a rectangle

Six of the shapes here are rep-tiles. The three similar rep-tiles here in blue, brown and black, are different from but similar to the six large rep-tiles in the first illustration at the beginning of the first post in this series.

Also, apart from those six rep-tiles there is an irrep-tile in the bottom left hand corner:

NEXT POST: Welcome To The Rep-Tile House Part 4

INFINITIES 7 – Welcome to the Rep-tile House Part 2 of 5

This is the seventh in a series of posts exploring infinity, entities and ideas infinite, infinities larger than other infinities, infinity paradoxes, infinite perimeters, infinite regress and infinite sequences such as cyclic numbers.

Illustration copyright M.W.F. YOUNG 2024

This is also the second in a series of posts about replicating tiles, or rep-tiles for short. Some rep-tiles are quite boring but some are very interesting. A rep-tile is a shape (e.g. a square) which can be divided into smaller shapes all of which are identical in shape to the figure you started with. Those identical smaller shapes are also all the same size. For more details see the first post in this series on rep-tiles.

There are seven rep-tiles in the illustration above. For example, take a look at the figure on the left at the top.

The overall large figure consists of nine squares, each of those squares consists of four smaller shapes (blue, orange, grey and brown), and each of those smaller shapes is identical in shape to the large overall shape you started with. You have thirty-six (9 x 4) of the smaller shapes inside the large shape. Not only that, but all thirty-six smaller shapes are all the same size. This large shape is a rep-tile.

THE TRIAL OF GIORDANO BRUNO
By Jastrow – Self-photographed, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1193142

All seven rep-tiles here consist of nine squares and each square is divided up into four smaller shapes. The text consists of historical dates and events that happened during each year listed. For example, the Roman emperor Marcus Aurelius was born in 121 CE. In 1600 Dominican friar and later cosmologist Giordano Bruno is burned at the stake for heresy. He had insisted that the universe was infinite and therefore could have no centre. He also rejected the afterlife, the Trinity and other central church doctrines. The entry under the date 2025 is speculative.

With these rep-tiles we have squares made up of small rep-tiles and large rep-tiles made up of squares – squareness is the name of the game. Have you guessed the significance of all these dates / numbers? The dates / numbers are themselves perfect squares: 121 = 11 x 11. 1600 = 40 x 40. 1936 = 44 x 44 and so on. You might want to test your number sense by going through and trying to guess what the square root of each date / number is.

Did you also notice the four numbers at the bottom without text – 5, 25, 625, 390625? It seems that if you square 5 you get 25 and the last digit of 25 is 5. If you square 25 you get 625 and the last two digits of 625 are 25. If you square 625 you get 390625, and the last three digits of 390625 are 625.

SPHINX

There is also something called an IRREP-TILE which is an IRREGULAR REPLICATING TILE. An irrep-tile, like a rep-tile, is a shape which can be subdivided into smaller shapes all of which are identical to the large shape you started with. However, those smaller shapes are not all the same size. In the illustration above, featuring a shape which mathematicians refer to as The Sphinx, you can see four rep-tiles at the bottom which are four different ways in which the sphinx shape can be subdivided into nine identical smaller sphinxes.

However, every rep-tile, not just this one, can be turned into an irrep-tile, as illustrated by the main figure in this illustration. In this main figure one can see that the Sphinx has been subdivided into four smaller sphinxes, separated here by thin white lines. However, any one of those four (in this case the darkest one) can be subdivided into four smaller sphinxes, and any or all of those four smaller ones can be subdivided further, and so on forever until the shapes are infinitesimally small.

This is my illustration of another irrep-tile. I started with a configuration of four squares in the shape of a sort of stubby upside-down T shape. Each one of those four squares can be subdivided into four smaller T-shapes identical to the original large T-shape. The T-shape, treated as a rep-tile, can therefore be subdivided into sixteen smaller shapes identical to the original and all the same size. I’ve subdivided just the three bottom squares each into four smaller T-shapes, each one in the form of part of a maze:

By the way this maze is a legitimate maze, with an entrance and an exit and a way to get from one to the other. I also subdivided the fourth square, at the top, into four smaller T-shapes (divided by thin white lines):

However in this case I subdivided two of those four T-shapes (at the bottom and on the right) into sixteen smaller T-shapes – in the bottom case two dark blue, two light blue, six brown and six orange T-shapes, and in the case on the right six dark blue, six light blue, two brown and two orange T-shapes.

In the case of the last two T-shapes (on the left and at the top) in the square at the top, in each case I subdivided the T-shape into fourteen smaller T-shapes plus two other T-shapes each of which has been subdivided further into sixteen white T-shapes.

I could have kept subdividing forever until the shapes were infinitesimally small. On the other hand I could have just divided the original large inverted T-shape into sixteen smaller T-shapes in the form of one large maze.

NEXT POST: Welcome To The Rep-Tile House Part 3

INFINITIES 6 – Welcome to the Rep-tile House Part 1 of 5

This is the sixth in a series of posts exploring infinity, entities and ideas infinite, infinities larger than other infinities, infinity paradoxes, infinite perimeters, infinite regress and infinite sequences such as cyclic numbers.

The term rep-tile was coined by Solomon W. Golomb, an abbreviated word based on the phrase REPLICATING TILE. The simplest rep-tile is a square. If you take a square and join the mid-points of opposite sides you end up with four smaller shapes all the same shape as the large square you started with, and they are all also the same size. Therefore the square is a rep-tile. The same thing works with any rectangle, parallelogram, rhombus and equilateral triangle. Boring. However in the illustration at the top of this post is a set of six rep-tiles which are all a lot more interesting than a square. In each case the large shape can be divided up into smaller shapes all of which are the same shape as the shape you started with, and all of those smaller identical shapes are also the same size.

In every illustration I have inserted a reptile, in this case a gecko. The bee on the left is called Slim Harpo – it was Slim Harpo (real name: James Moore) who composed and recorded the song called ‘I’m a King Bee’, later covered by The Rolling Stones, among others.

Also, the bee on the right has a tag attached to it reading “IF FOUND PLEASE RETURN TO SHERLOCK HOLMES”. When Sir Arthur Conan Doyle had his creation, Sherlock Holmes, retire to the Sussex Downs in his later years, Doyle tells us that one of the things that fascinated him in his retirement was his study of the segregation of the queen in bee hives.

Then there’s the queen bee labelled Queen Elizabeth.

THE REAL QUEEN ELIZABETH II.
By Ministry of Information official photographer – http://media.iwm.org.uk/iwm/mediaLib//20/media-20543/large.jpgThis photograph TR 2832 comes from the collections of the Imperial War Museums., Public Domain, https://commons.wikimedia.org/w/index.php?curid=24396386

ISOSCELES RIGHT-ANGLED TRIANGLES

In this second illustration, there are seven rep-tiles all constructed out of isosceles right-angled triangles. For example, take the shape at the top on the left.

It consists of four connected isosceles right-angled triangles each of which is subdivided into smaller blue and yellow isosceles right-angled triangles. If you examine any of these eight configurations of smaller triangles (four blue and four yellow) you’ll discover that each is identical in shape to the large shape you started with originally.

This figure in the middle on the right, with the smaller triangles, is particularly ingenious. The rep-tile just below that one is also interesting in that each of the eight smaller sets of yellow and blue triangles (two in each set) can also be viewed as four sets of yellow and blue triangles (four in each set) each of which consists of rep-tiles identical to the large shape on the left at the top of the main illustration (the first rep-tile discussed above):

The preponderance of RIGHT-angled triangles led to the idea of adding phrases which include the word RIGHT. Do The Right Thing is a landmark 1989 feature film produced, written and directed by Spike Lee. Right Now is a wonderful sort of ingenious meta-music video released by Van Halen in 1991 – https://www.youtube.com/watch?v=gU7d2EHV_OQ&ab_channel=VanHalen . I’m All Right, Jack is a 1959 British film starring Peter Sellers who won a BAFTA for his performance in the film. The Right Stuff was a 1983 film about the test pilots selected to be astronauts, all of them male, as part of the misogynist early American space program (though the film seems to have overlooked the misogyny). For more details see my previous post here – https://thekiddca.wordpress.com/2021/07/31/negative-space/ .

SQUARES

In this final illustration, everything is based on squares. On the left at the top the large shape consists of eight smaller squares, and each smaller square is divided up into an orange shape and a green shape, making sixteen smaller shapes in all. Each of those sixteen smaller shapes is identical to the large shape you started with.

The same thing applies to the other shapes across the top. The trick is figuring out how to divide a square into two identical halves each of which consists of eight small squares.

On the second row we have fourteen large L-shaped rep-tiles each of which is sub-divided into nine smaller L-shapes, which can be done in fourteen different ways as illustrated here.

Each large L-shape could also be sub-divided into four identical squares. The illustration also shows that one can put four large L-shapes together to create a large square, like the three pictured here.

NATHAN PHILLIPS SQUARE, TORONTO.
By Hutima – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=121721123

The rest of the illustration runs with the concept of squareness, e.g. the sailing ship is a square rigger.

In the vicinity of that ship are various square-related entities from the field of Mathematics. At the bottom are the names of various famous squares:

Trafalgar Square in London, England – with Nelson’s Column surrounded by lions
St. Peter’s Square in Vatican City, Italy – fronting St. Peter’s Basilica, home of the Pieta
Tiananmen Square in Beijing, China – where Mao Zedong proclaimed the birth of modern China in 1949, and many died in 1989
Leicester Square in London, England – referenced in songs, including Jeffrey Goes to Leicester Square (Jethro Tull), It’s a Long Way to Tipperary (from World War One), and a rather graphic song by The Rolling Stones
St. Mark’s Square in Venice, Italy – which Napoleon called the drawing room of Europe
Nathan Philips Square in Toronto, Canada – site of many an anti-war demonstration
Wenceslas Square in Prague, The Czech Republic – site of demonstrations of more than a hundred thousand people during the Velvet Revolution
Red Square in Moscow, Russia – site of Lenin’s Tomb and St. Basil’s Cathedral

ONE OF THE LIONS AT THE BASE OF NELSON’S COLUMN IN TRAFALGAR SQUARE, WITH BIG BEN IN THE BACKGROUND
By Florinux – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12463608

There’s a square knot in the bottom right hand corner, and a variety of mathematical and linguistic squares. In the four magic squares on the left all numbers in all of the rows, columns and diagonals add up to the same number.

These squares exhibit other interesting mathematical properties as well, e.g. in the magic square at the top on the right, if you reverse the digits in all 16 numbers (96 becomes 69 etc.) you still end up with a magic square.

In the set of four squares on the right, each row, column and diagonal of the top left square, a Latin square, contain all four digits – 1, 2, 3 and 4.

In the word square on the right at the top, the four words reading across (card, area, rear, dark) are repeated reading down. In the bottom left word square there are four words reading across, but four different English words reading down. In the last word square there are four words reading across (tans, area, lion, land), four different words reading down (tall, aria, neon, sand), and two words reading diagonally (trod, lies).

NEXT POST: Welcome To The Rep-Tile House Part 2

Post 1 – https://thekiddca.wordpress.com/2024/04/06/infinities-infinity-everywhere/

Post 2 – https://thekiddca.wordpress.com/2024/04/13/infinities-2-theres-no-business-like-snow-business/

Post 3 – https://thekiddca.wordpress.com/2024/04/20/infinities-3-infinitesimal-chi-chiao-tu/

Post 4 – https://thekiddca.wordpress.com/2024/04/27/infinities-4-no-vacancies-but-rooms-still-available-at-hotel-infinity/

Post 5 – https://thekiddca.wordpress.com/2024/05/04/infinities-5-pythagorean-infinity/