
This is the first in a series of posts exploring infinity. There will be one infinity larger than another infinity, infinite perimeters, infinite regress, infinity paradoxes, an infinite set of bizarre things called cyclic numbers, and other infinity-related concepts.
Infinities (and infinitesimals) are everywhere. Start counting (1 2 3 . . . ) and see how far you get. If the word “universe” means everything that exists, the universe must be infinitely large as well. It would also seem that Time is eternal, that is it consists of an infinite number of seconds or minutes or decades or whatever arbitrary unit of time you wish to use. Cosmologists are not all in agreement with these concepts, however, depending on how you define the words “exists”, “time” and “spacetime”.
Some infinities are different than others. If, for example, I start adding up the Natural Numbers (1 + 2 + 3 + 4 + . . . ), and did that forever, I would end up with an infinitely large number. This is a divergent infinite series. On the other hand, if I start adding up a series of ever smaller fractions ( 1/2 + 1/4 + 1/8 + 1/16 + . . . ) I could also do that forever, but in this case I would never get to the number one, let alone an infinitely large number. This is a convergent series, and involves the concept of being infinitesimally small.
Infinity is not a number but a condition of endlessness. It is a slippery concept. For example, infinity plus infinity equals infinity. The set of odd numbers is obviously infinite, and so is the set of even numbers, and if you combine the two sets you get the set of Natural Numbers which is also infinite. However the set of even numbers and Natural Numbers are the same size even though there seem to be only half as many even numbers as there are Natural Numbers. We know these two sets are the same size because we can match the Natural Number one up with the even number two, the Natural Number two with the even number four, three with six and so on, doubling each time, so we know that both sets have the same number of numbers in them.
What is even stranger is that some infinities are larger than others. I’ve understood the proof of that fact (it’s not a difficult proof) but I still can’t get my head around that idea. How can you have a number greater than the number of Natural Numbers? Georg Cantor proved it was possible, over a century ago. He showed that the number of Real Numbers is greater than the number of Natural Numbers, which means that the number of Transcendental Numbers (pi is a transcendental number, for example) is also greater than the number of Natural Numbers.
INFINITE SETS
Infinity is tricky. I can use infinite sets to prove that 1/2 = 0, and all the Natural Numbers (1, 2, 3 . . . ) not only add up to -1/12 but they also add up to -1/8 so I guess -1/12 = -1/8. The proofs use simple arithmetic and I have placed them at the end of this post if you want to take a look at them and try to figure out why they seem to be correct even though they “prove” something obviously false.
ACHILLES AND THE TURTLE
About 2500 years ago the Greek philosopher Zeno of Elea (490 BCE – 430 BCE) argued that if the great athlete Achilles was running a Kilometre long race against a turtle, and the turtle was given just a short head start of, say, ten metres, then Achilles could never catch up let alone pass the turtle. Zeno explains that if the turtle gets to start at some point A, ten metres ahead of the starting line, then as soon as the race starts Achilles will soon catch up and also reach point A but in the time it takes for him to do so, the turtle will have advanced to some further point, call it point B. Then as Achilles runs from A to B the turtle will have advanced once more to some further point, call it point C. As this same process unfolds over and over again Achilles never catches up to the turtle.

THE PLATONIC SOLIDS IN THE FORM OF DICE
By Tomruen – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=39985790
INFINITELY NESTED PLATONIC SOLIDS
There is a set of five fascinating three dimensional solids called the Platonic Solids. One of them, with six sides, is called a hexahedron which is just a mathematical name for a cube. If you find the centres of the six sides of a hexahedron and connect those centres using triangles you get another one of the Platonic Solids, an eight-sided figure called an octahedron and it looks like this:
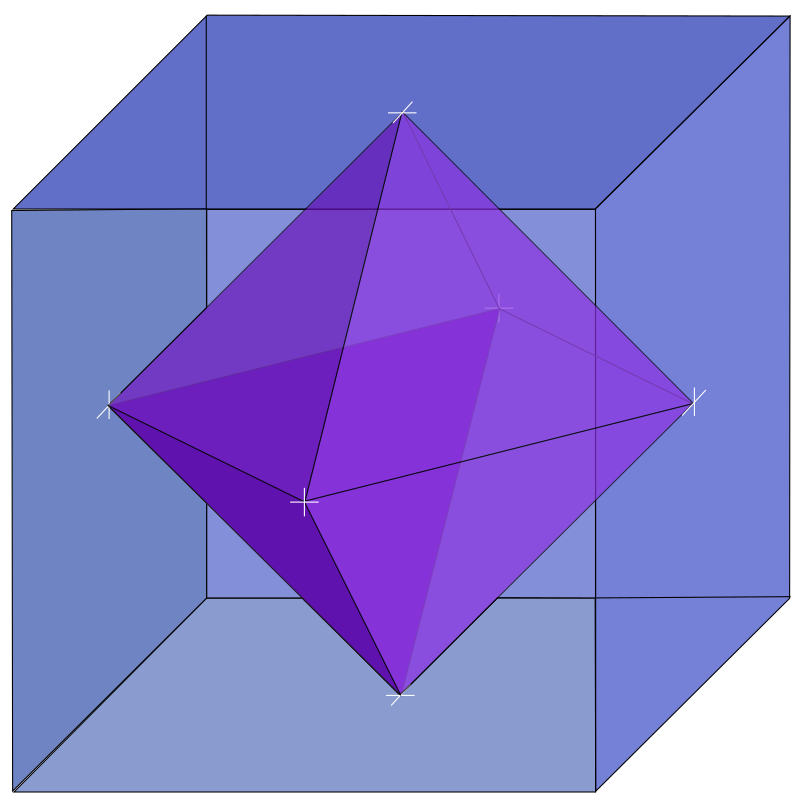
AN OCTAHEDRON INSIDE A HEXAHEDRON
By 4C – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1049163
Now, if you find the centres of the eight sides of that inner octahedron and connect those centres using squares you get another, smaller, hexahedron. Then you can fit an even smaller, second octahedron inside that smaller hexahedron, and keep forming smaller and smaller Platonic solids forever, alternating between hexahedra and octahedra. The shapes become infinitesimal. You can do the same thing with two other Platonic Solids – the twelve-sided dodecahedron and the twenty-sided icosahedron. I wonder what happens if you connect the centres of the sides of the last and simplest Platonic Solid, the four-sided tetrahedron, using triangles?
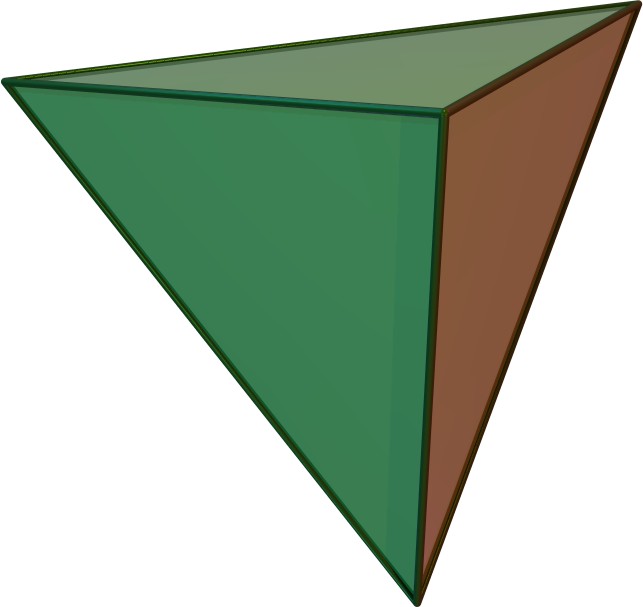
TETRAHEDRON
By The original uploader was Cyp at English Wikipedia. – en:User:Cyp/Poly.pov, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=38709
PI UNEXPECTEDLY
Not only does pi equal an infinitely non-terminating non-repeating decimal, it also shows up in the most unexpected places, such as Buffon’s Needle Problem – https://en.wikipedia.org/wiki/Buffon%27s_needle_problem . It can also be expressed as an infinite series in a variety of ways which seem to have nothing to do with circle ratios. For example:
- pi = 4(1/1 – 1/3 + 1/5 – 1/7 + . . . )
- pi = 2(2 x 2 x 4 x 4 x 6 x 6 x …) / (1 x 1 x 3 x 3 x 5 x 5 x …)
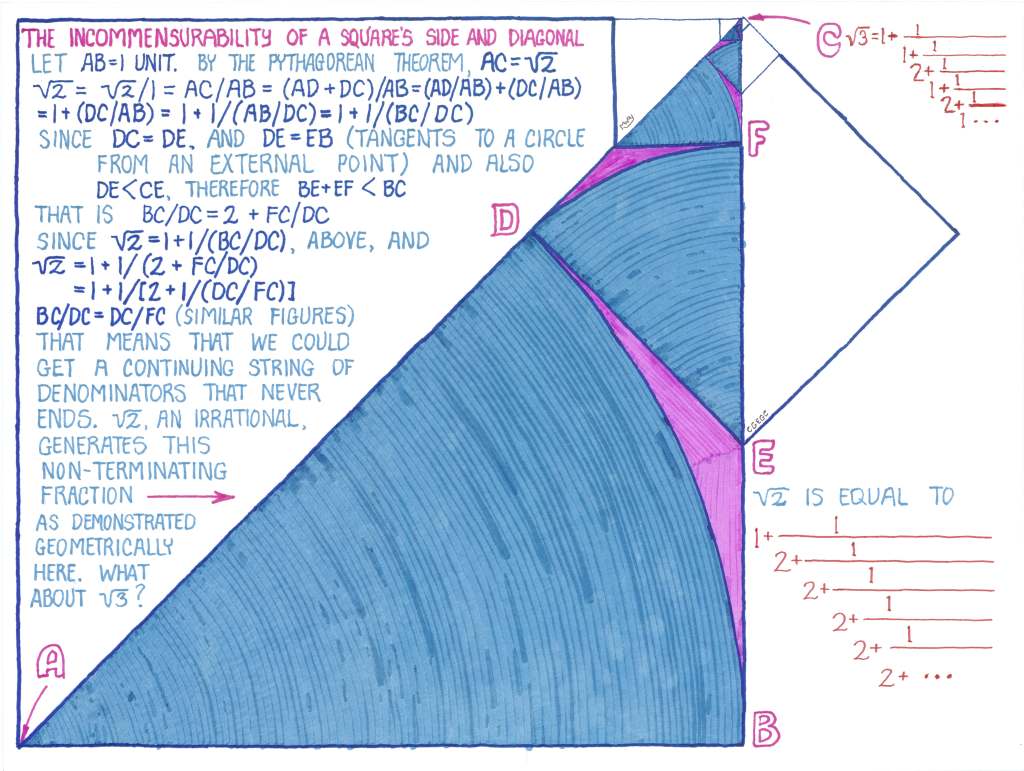
AN INFINITE CONTINUED FRACTION
Here is a geometric proof that the square root of two is equal to an infinite continued fraction. This was taken from the book Through The Mathescope by Stanley Ogilvy.
ASYMPTOTES
Some curves when graphed get closer and closer to their asymptotes (which are usually, but not always, straight lines) and so they go on forever. The two branches of a hyperbola never reach their asymptotes. The witch of Agnesi, a curve analysed at length by Maria Agnesi (1718 – 1799), approaches asymptotes along the positive and negative x axes but never reaches them, as illustrated here:
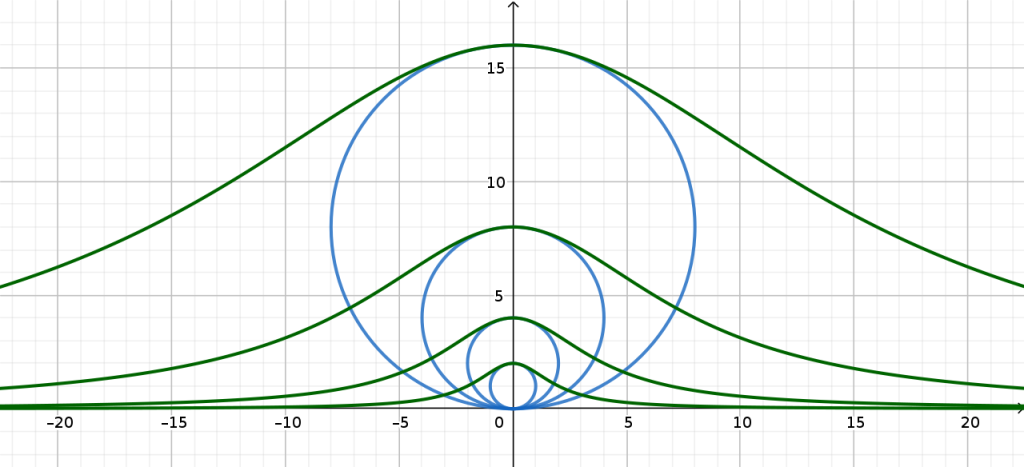
By Dicklyon – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=118532845
In trigonometry the tangent function becomes infinite when x equals π / 2, 3π/2, 5π/2 and so on, getting ever closer to their asymptote positive and negatively but never getting there. I have illustrated that phenomenon in this illustration:
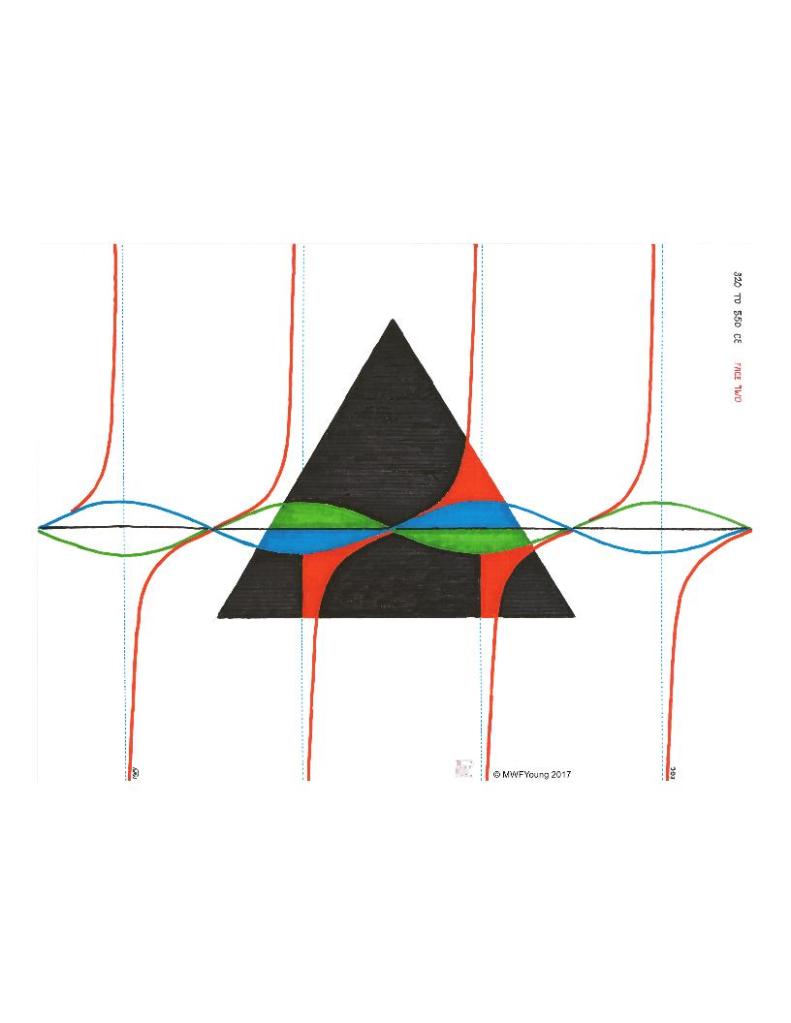
SOME NUMBER SETS THAT GO ON FOREVER
- Natural Numbers (1, 2, 3, 4 . . . )
- Integers (. . . -4, -3, -2, -1, 0, 1, 2, 3, 4 . . .)
- Odd Numbers (1, 3, 5, 7 . . .)
- Even Numbers (2, 4, 6, 8 . . .)
- Prime Numbers (2, 3, 5, 7 . . .)
- Perfect Squares (1, 4, 9, 16 . . .)
- Perfect Cubes (1, 8, 27, 64 . . .)
- and fourth powers, fifth powers and so on
- Triangular Numbers (1, 3, 6, 10 . . .)
- and Pentagonal Numbers, Hexagonal Numbers and so on
- Perfect Numbers (6, 28, 496, 8128 . . .)
- Cyclic Numbers (142857, 0588235294117647 . . .)
SOME INFINITE DECIMAL EXPANSIONS
The decimal forms of all sorts of numbers also go on to infinity.
- 4 = 4.0000000000 . . .
- 1/2 = 0.5000000000 . . .
- 1/9 = 0.1111111111 . . .
- 1/3 = 0.3333333333 . . .
- 1/7 = 0.142857 142857 142857 . . .
Some go on forever without repeating and are the roots of a non-zero polynomial of finite degree with rational coefficients (i.e. algebraic numbers):
- The square root two = 1.4142135623 . . .
- The square root of three = 1.7320508075 . . .
- The Golden Ratio / phi = 1.6180339887 . . . which is equal to one plus the square root of five all divided by two. It is the positive root of the equation x2 – x – 1 .
Some numbers go on forever without repeating but are not the roots of a non-zero polynomial of finite degree with rational coefficients (i.e. transcendental numbers):
- Pi = 3.1415926535 . . . which is the ratio of the circumference of a circle to its diameter.
- e = 2.7182818284 . . . which is the base of the natural logarithms aka Euler’s Number
- The Liouville constant = 0.1100010000 . . .
FINALLY, DIVISION BY ZERO
In Mathematics division by zero is said to be undefined. Some people have got the impression that one divided by zero equals infinity, but this implies that infinity is a number but it is not. To say that the limit of one divided by x approaches infinity as x approaches zero makes more sense, but that still doesn’t make it clear exactly why division by zero is undefined. It is undefined because if you accept it you end up with inconsistent results.
To illustrate, take the equation y = 1 / x. Graph this on a Cartesian coordinate system. What happens to y as x gets smaller and smaller, i.e. it approaches zero, but along the positive x-axis? Is the limit simply infinity? No it isn’t. Set x equal to 1 / 2 and y equals 2. Set x equal to 1 / 3 and y equals 3. Set x equal to 1 / 1000000 and y equals 1000000. In other words, the limit is positive infinity. Again have x get smaller and smaller as it approaches zero, but have it approach zero along the negative x-axis this time. What happens? Set x equal to -1 / 2 and y equals -2. Set x equal to -1 / 3 and y equals -3. Set x = -1 / 1000000 and y equals -1000000. In other words, the limit is negative infinity. So, even if you try to figure out what the limit of 1 / x is as x approaches zero, you get that the limit is simultaneously positive and negative infinity, which is mathematically meaningless, inconsistent and ridiculous. If you graph the function you have two simultaneous curves, one going up forever and the other going down forever, both of them asymptotic to the y-axis. So don’t divide by zero. Just don’t.
NEXT POST: A curve with an infinite perimeter and a finite area.
PROOF THAT 1/2 = 0, AND -1/12 = -1/8 (AND THEREFORE EVERY WHOLE NUMBER IS EQUAL TO EVERY OTHER WHOLE NUMBER)
INFINITE SET 1. Let me show you that 1/2 = 0
- Let A = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 . . .
- 1 – A = 1 – (1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 . . . )
- 1 – A = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 . . .
- 1 – A = A
- 1 = 2A
- A = 1/2
But wait a minute:
- A = 1 – 1 + 1 – 1 + 1 – 1 +1 – 1 . . .
- A = (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) . . .
- A = 0 + 0 + 0 + 0 . . .
- So A is also equal to 0. Apparently 1/2 = 0.
INFINITE SET 2
- Let B = 1 + 2 + 3 + 4 + . . .
- Let S = 1 – 2 + 3 – 4 + 5 – 6 . . .
- B – S = (1 – 1) + (+2 – (-2) ) + (+3 – (+3) ) + (+4 – (-4) ) + . . .
- B – S = 0 + 4 + 0 + 8 + 0 + 12 + . . .
- B – S = 4(1 + 2 + 3 + 4 + . . . )
- B – S = 4B
Now we need to find out what S equals. Add S to itself but when you put the second S under the first shift it over so that the 1 in the second S is under the 2 in the first S, the 2 in the second S is under the 3 in the first S and so on.
- 2S = 1 + [(-2) + (+1)] + [(+3) + (– 2) ] + [(-4) + (+3)] + . . .
- 2S = 1 – 1 + 1 – 1 + 1 – 1 + . . .
- But we found out above that A = 1 – 1 + 1 – 1 + 1 – 1 . . . = 1/2
- So 2S = A = 1/2
- S = 1/4
- Now go back to the line B – S = 4B
- B – 1/4 = 4B
- B – 4B = 1/4
- -3B = 1/4
- -12B = 1
- B = -1/12 = 1 + 2 + 3 + 4 + . . .
You can also use infinite series’ to prove that B is also equal to -1/8 if you like:
- B = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + . . .
- B = 1 + (2 + 3 + 4) + (5 + 6 + 7) + (8 + 9 + 10) + . . .
- B = 1 + 9 + 18 + 27 + . . .
- B = 1 = 9(1 + 2 + 3 + . . .)
- B = 1 + 9B
- B – 9B = 1
- -8B = 1
- B = -1/8
- If -1/12 = -1/8
- then 24(-1/12) = 24(-1/8)
- -2 = -3
- -2 + 2 = -3 + 2
- 0 = -1
You can now multiply both sides by -1 (so 0 = 1), or by -2 (so 0 = 2), or by -3 (so 0 = 3) and so on, so every Natural Number equals every other Natural Number and they are all equal to zero.