
This is the second of a series of posts exploring infinity. There will be one infinity larger than another infinity, infinite perimeters, infinite regress, infinity paradoxes, an infinite set of bizarre things called cyclic numbers, and other infinity-related concepts.
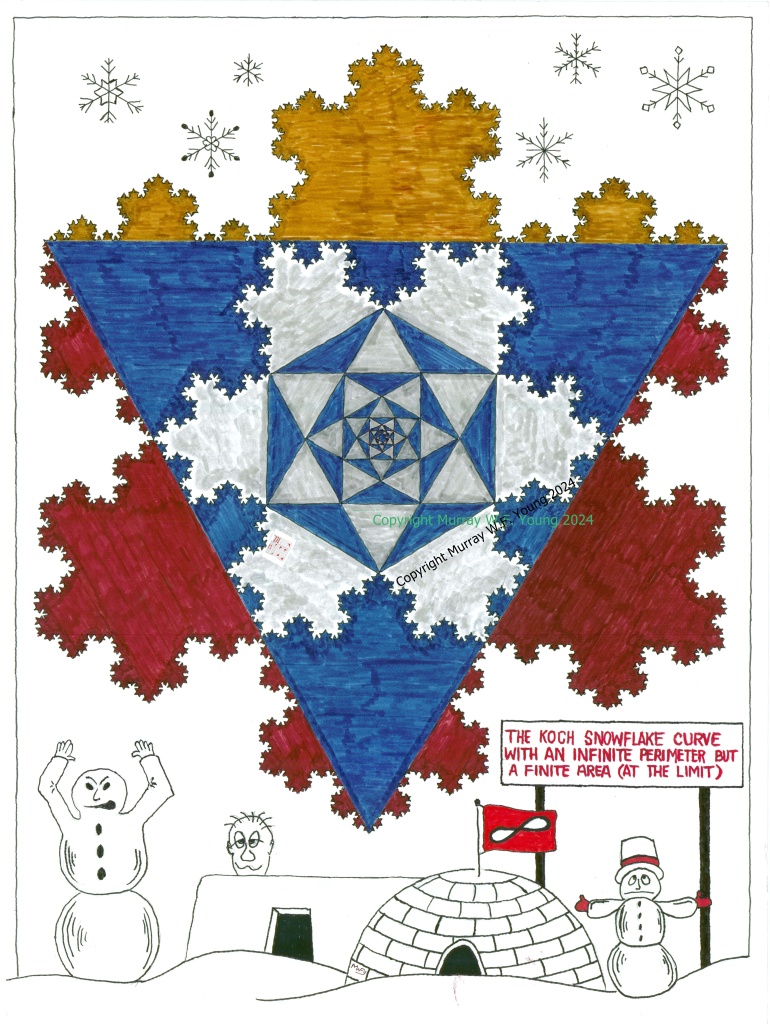
How could one possibly have a geometric shape that has an infinite perimeter but a finite area? That is exactly one of the properties of one of the first fractals ever analysed. I’m talking about the Snowflake Curve, discovered and analysed by Swedish mathematician Helge von Koch back in 1904. The outline around the outside of the shape illustrated above is the Snowflake Curve (this shape also consists of six smaller Snowflake Curves plus an area in the middle displaying a set of six-pointed stars which get infinitesimally smaller).
One can also tessellate the Euclidean two dimensional plane using this snowflake curve, that is, you can cover an infinite plane with snowflake shapes without leaving any spaces between snowflakes and without any overlapping figures, however, you need to use two different sizes of snowflake.

TESSELATING THE PLANE WITH A SNOWFLAKE CURVE
By David Eppstein – Own work, CC0, https://commons.wikimedia.org/w/index.php?curid=16959022
It is extraordinary to think that one can have something with an infinite perimeter and finite area. Here is something even more extraordinary. Consider the dimension of the snowflake curve. A point has zero dimensions. A line has one dimension – length. A square has two dimensions – length and width. A cube has three dimensions – length, width and height. The concept of a fractional dimension doesn’t seem to make sense. However, consider the concept of a dimension as a measure of complexity. It turns out that the dimension of the snowflake curve is the natural logarithm of 4 divided by the natural logarithm of 3, and this equals approximately 1.26186 . Extraordinary.
Like all good fractals, a snowflake curve is also infinitely self-similar. That is, if you zoom in to any point on the edge of a snowflake curve you see smaller and smaller exact replicas of the original curve. In calculus, the first derivative of a curve at any point really just takes the form of the tangent to the curve at that point. However, a snowflake curve has no tangents, and therefore no derivatives. That’s rather extraordinary as well. There are variations of the snowflake curve using angles other than sixty degrees, and there are even three dimensional versions of the snowflake curve. There’s also the Minkowski Sausage.

THE MINKOWSKI SAUSAGE
By AnonymousBosch – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17891107
There’s also Gabriel’s horn (also known as Torricelli’s trumpet). This is a three dimensional entity whose volume is finite yet its surface area is infinite.
Here’s how you construct this curve, and if you follow these steps an infinite number of times you end up with a closed shape with an infinite perimeter but a finite area. Start with an equilateral triangle with each side, say, 27 units long (or any length you like). Now use this algorithm: erect a new equilateral triangle in the middle of each side of this shape and erase the bottom of the new triangle. That is, divide each side into three equal sections (each one is therefore 9 units long) and on the middle section of each side erect another equilateral triangle and erase its baseline. This new overall shape will have twelve sides each nine units long (a six pointed star). You have just completed the first iteration of the algorithm. Use the algorithm again, erect a new equilateral triangle in the middle of each side of this new shape and erase the bottom of each new triangle. This gives you a 48-sided shape and each side is 3 units long. If you follow the algorithm again you have a 192-sided shape and each side is one unit long. Simply do this forever. Take your time. The shape pictured above has only gone through six iterations.
Each step increases the perimeter by four thirds and the length of the curve after n iterations is four-thirds to the nth power. These steps generate a divergent infinite series so the limit after an infinite number of iterations is infinity. It also turns out that after an infinite number of iterations the area of the snowflake is exactly eight-fifths times the area of the original triangle, a finite value.
I have in my mathematical library a rather unusual book. It is a science fiction novel titled “The Curve of the Snowflake” by William Grey Walter, an American neurophysiologist, cybernetician and robotician who was raised in Britain from the age of five. He is known for his construction of some of the first electronic autonomous robots in the 1940’s. From the dust cover: “Not since H.G.Wells has a writer combined such a variety of intellectual and scientific brilliance with so clear and witty a talent for fiction. The Curve of the Snowflake is a novel of both delight and true importance. The snowflake curve is a paradox which can be described and constructed by science but not yet explained. It is the device of this novel.”
By the way, a figure with an infinite perimeter is called a teragon, a term coined by Benoit Mandelbrot who also coined the term fractal and was the first to analyse fractals at an advanced level. An infin-tile is also a teragon, one that I will talk a bit about in a later post. Here is another snowflake curve I drew a few years ago.
NEXT POST: Infinitely regressive tangrams
Post 1 – https://thekiddca.wordpress.com/2024/04/06/infinities-infinity-everywhere/